| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 우선순위 큐
- DP
- 비트마스크
- lis
- 그리디
- 중복 순열
- 백트래킹
- Knapsack
- 클래스
- 분할 정복
- 문자열
- BFS
- 스택
- 조합
- BeautifulSoup
- 크루스칼
- 피보나치 수
- 세그먼트 트리
- 시뮬레이션
- 재귀
- dfs
- 빠른 입출력
- 순열
- 메모리풀
- 완전 탐색
- 링크드리스트
- SSAFY
- 큐
- MST
- 이분 탐색
- Today
- Total
작심 24/7
[백준] 9029번 정육면체 본문
9029번: 정육면체
입력은 표준입력(standard input)을 통해 받아들인다. 입력의 첫 줄에는 테스트 케이스의 개수 T (1 ≤ T ≤ 20) 가 주어진다. 각 테스트 케이스에 대해 원목의 크기를 나타내는 W,L,H (1 ≤ W, L, H ≤ 200) ��
www.acmicpc.net
규칙을 찾으면서 너무 어렵게 생각하려고 하면 풀기 힘든 문제이다.
DP로 W, L, H가 1, 1, 1일 때부터 200, 200, 200일 때까지 값을 모두 구해놓고 풀어야 한다.
설명하자면,

이렇게 그림에 나와있는 것처럼 직육면체를 두 조각으로 자르는 것에 주목해보자
H를 1 기준으로 자른 조각들은 W, L, 1와 W, L, H-1가 되고
W, L, 1에서 얻을 수 있는 정육면체의 최소 개수와
W, L, H-1에서 얻을 수 있는 정육면체의 최소 개수를 더한 값을 A라 하고
H를 2 기준으로 자른 조각들은 W, L, 2와 W, L, H-2가 되고
W, L, 2에서 얻을 수 있는 정육면체의 최소 개수와
W, L, H-2에서 얻을 수 있는 정육면체의 최소 개수를 더한 값을 B라고 하자
이런 식으로 기준이 H/2가 될 때까지 잘라서 나온 값들 A, B, ... 중 가장 작은 값이
H를 기준으로 잘랐을 때 W, L, H에서 얻을 수 있는 정육면체의 최소 개수가 된다.
이렇게 W와 L도 기준으로 잡고 똑같이 자르며 비교해주면
최종적으로 W, L, H에서 얻을 수 있는 정육면체의 최소 개수를 얻을 수 있게 된다.
예를 들어 W, L, H가 2, 4, 3일 때,

W를 기준으로 절단하는 경우

L을 기준으로 절단하는 경우
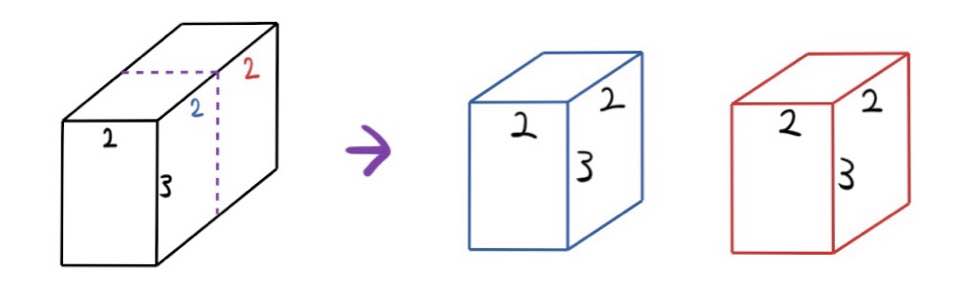

H를 기준으로 절단하는 경우
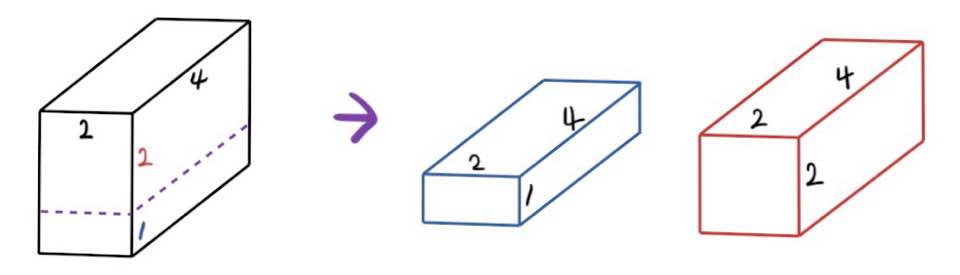
이렇게 나온 조각들은 각자 최소 개수가 저장되어 있는 상태이므로
그 값들을 더한 값들 중 최솟값을 저장하면 되는 것이다.
이 방식을 적용하려면 4중 for문이 필요하다.
(그래서 시간제한이 10초나 되나 보다)
이때 주의할 점은 W, L, H의 길이가 모두 같을 땐 자를 필요 없는 정육면체이므로 값이 1이 된다.
이 경우만 따로 걸러주면 되는데
나는 시간 초과될까 봐 W, L, H 중 하나라도 1일 경우와
두 길이가 나머지 하나의 배수인 경우를 걸러주고
W, L, H의 순서만 다를 경우엔 어차피 다 값이 똑같으므로
순서만 다른 경우 모두 그 값을 넣어주었다.
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int cube[201][201][201] = { 0 };
for (int w = 1; w <= 200; w++) {
for (int l = 1; l <= 200; l++) {
for (int h = 1; h <= 200; h++) {
if (!cube[w][l][h]) { //값이 이미 채워져 있으면 굳이 돌릴 필요 없다
if (w == 1) cube[w][l][h] = l * h;
else if (l == 1) cube[w][l][h] = w * h;
else if (h == 1) cube[w][l][h] = w * l;
else if (w % h == 0 && l % h == 0) cube[w][l][h] = (w / h) * (l / h);
else if (w % l == 0 && h % l == 0) cube[w][l][h] = (w / l) * (h / l);
else if (l % w == 0 && h % w == 0) cube[w][l][h] = (l / w) * (h / w);
else {
cube[w][l][h] = 1000000000;
for (int i = 1; i <= w / 2; i++) //가로를 기준으로 쪼갠다
cube[w][l][h] = min(cube[w][l][h], cube[i][l][h] + cube[w - i][l][h]);
for (int i = 1; i <= l / 2; i++) //세로를 기준으로 쪼갠다
cube[w][l][h] = min(cube[w][l][h], cube[w][i][h] + cube[w][l - i][h]);
for (int i = 1; i <= h / 2; i++) //높이를 기준으로 쪼갠다
cube[w][l][h] = min(cube[w][l][h], cube[w][l][i] + cube[w][l][h - i]);
}
cube[w][h][l] = cube[l][w][h] = cube[l][h][w] = cube[h][w][l] = cube[h][l][w] = cube[w][l][h]; //가로 세로 높이의 순서가 바뀌어도 값은 똑같으므로
}
}
}
}
int T, W, L, H;
cin >> T;
for (int t = 0; t < T; t++) {
cin >> W >> L >> H;
cout << cube[W][L][H] << "\n";
}
return 0;
}'백준' 카테고리의 다른 글
| [백준] 2178번 미로 탐색 (0) | 2020.06.15 |
|---|---|
| [백준] 2644번 촌수계산 (0) | 2020.06.15 |
| [백준] 2468번 안전 영역 (C++, JAVA) (0) | 2020.06.10 |
| [백준] 10026번 적록색약 (C++, JAVA) (0) | 2020.06.10 |
| [백준] 11403번 경로 찾기 (C++, JAVA) (0) | 2020.06.10 |