| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Knapsack
- 완전 탐색
- MST
- 조합
- 피보나치 수
- 클래스
- 백트래킹
- 스택
- 비트마스크
- 중복 순열
- 링크드리스트
- SSAFY
- DP
- 시뮬레이션
- dfs
- 분할 정복
- BFS
- 그리디
- 큐
- BeautifulSoup
- 빠른 입출력
- 재귀
- 우선순위 큐
- 문자열
- 이분 탐색
- 크루스칼
- 세그먼트 트리
- 순열
- 메모리풀
- lis
- Today
- Total
작심 24/7
[프로그래머스] 지형 이동 Summer/Winter Coding(2019) 본문
코딩테스트 연습 - 지형 이동
[[1, 4, 8, 10], [5, 5, 5, 5], [10, 10, 10, 10], [10, 10, 10, 20]] 3 15 [[10, 11, 10, 11], [2, 21, 20, 10], [1, 20, 21, 11], [2, 1, 2, 1]] 1 18
programmers.co.kr
이 문제는 풀이를 찾아보면서 공부하며 풀었다.
여기 친절히 설명되어 있는 공식 해설을 첨부한다.
[2019 윈터코딩] 가장 어려웠던 코딩테스트 3번 문제 해설
스타트업에서 개발자 커리어를 시작하고픈 수많은 주니어들에게 꾸준한 채용 등용문이 되어주고 있는, 프로그래머스의 윈터코딩(Winter coding). 현재 1차 코딩테스트와 2차 실무 과제 제출을 모두
prgms.tistory.com
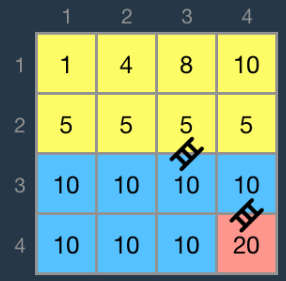
상세 풀이는 이렇다.
1. bfs를 이용하여 사다리 없이 이동할 수 있는 영역들을 그룹화시킨다.
- main문에서 NxN 배열 for문을 돌려 그룹화되어 있지 않은 원소들만 bfs함수를 호출시킨다.
- bfs함수에서 height 이하인 상하좌우로 근접한 원소들을 큐에 넣었다 뺐다 하며 그룹화시킨다.
- main문으로 돌아오면 그 다음 그룹을 위해 그룹번호+1을 해준다.
2 서로 다른 그룹 사이를 이동할 때 필요한 비용을 (노드1, 노드2, 간선) 형식으로 구한다.
- 노드 두개와 간선 하나를 저장해야 하므로 Edge 클래스를 만들어 형식을 지정한다.
- findHeight함수에서 Edge 타입으로 정의한 벡터에 값들을 저장한다.
3. 크루스칼 알고리즘을 이용해 최소 스패닝 트리(MST)를 구한다.
- height 값을 기준으로 벡터를 오름차순 정렬한다.
- 1차원 배열 parent를 만들어 각 노드가 부모로 자기 자신을 가리키도록 초기화한다.
- check 함수를 통해 양 끝 노드의 부모 노드가 같아 사이클이 생기는지 여부를 가려준다.
- 사이클이 아닌 경우에만 union-find로 부모 노드를 통일시켜준다.
- 이때 해당하는 height들을 합해서 answer에 넣어주면 끝
#include <iostream>
#include <queue>
#include <string>
#include <vector>
#include <cstdlib>
#include <algorithm>
using namespace std;
queue <pair<int, int>> q; //인덱스 값 넣어줌
int nearby[4][4] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} }; //상하좌우 비교 위해
//실제 부모 노드를 찾는 함수
int FindParent(int parent[], int x) {
if (parent[x] == x)return x; //root인 애는 자기 자신을 부모로 가지고 있음
return parent[x] = FindParent(parent, parent[x]); //아닐 시 재귀로 부모 찾아줌
}
//두 부모 노드를 통일시키는 함수
void UnionParent(int parent[], int a, int b) {
a = FindParent(parent, a);
b = FindParent(parent, b);
if (a < b)parent[b] = a; //항상 큰 인자가 작은 인자를 부모로 가짐
else parent[a] = b;
}
//같은 부모를 가지는지 확인하는 함수
int Check(int parent[], int a, int b) {
a = FindParent(parent, a);
b = FindParent(parent, b);
if (a == b)return 1;
else return 0;
}
//간선 클래스
class Edge {
public:
int node[2];
int distance;
Edge(int a, int b, int distance) { //초기화를 위한 생성자 함수
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
bool operator <(Edge &edge) { //간선 기준 오름차순 정렬을 위해 연산자 '<' 오버로딩
return this->distance < edge.distance;
}
};
void Bfs(int N, int height, int arr[][303], int i, int j, int group[][303], int group_num) {
q.push(make_pair(i, j));
while (!q.empty()) {
pair<int, int>temp = q.front();
int x = temp.first, y = temp.second, a, b;
q.pop();
for (int n = 0; n < 4; n++) { //상하좌우 순으로 비교한다
a = x + nearby[n][0], b = y + nearby[n][1];
if (a >= 0 && a < N && b >= 0 && b < N && group[a][b] == 0 && abs(arr[x][y] - arr[a][b]) <= height) {
q.push(make_pair(a, b));
group[a][b] = group_num; //사다리 없이 갈 수 있는 칸끼리 그룹화
}
}
}
}
vector<Edge> v;
void FindHeight(int N, int arr[][303], int i, int j, int group[][303]) {
int a, b;
for (int n = 0; n < 4; n++) { //상하좌우 순으로 비교한다
a = i + nearby[n][0], b = j + nearby[n][1];
if (a >= 0 && a < N && b >= 0 && b < N && group[a][b] != group[i][j]) {
v.push_back(Edge(group[i][j], group[a][b], abs(arr[a][b] - arr[i][j]))); //다른 그룹 사이의 height를 벡터에 기록
}
}
}
int solution(vector<vector<int>> land, int height) {
int N = land.size(), group_num = 1;
int parent[1000010] = { 0 }, arr[303][303] = { 0 }, group[303][303] = { 0 };
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
arr[i][j] = land[i][j];
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (group[i][j] == 0) { //그룹화가 되어 있지 않을 때
group[i][j] = group_num;
Bfs(N, height, arr, i, j, group, group_num);
group_num++;
}
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
FindHeight(N, arr, i, j, group);
}
}
//크루스칼 알고리즘
sort(v.begin(), v.end()); //간선의 비용(height)를 기준으로 오름차순 정렬
int answer = 0;
for (int i = 0; i < group_num; i++)parent[i] = i; //처음에는 자기 자신을 부모로 가짐
for (int i = 0; i < v.size(); i++) {
if (Check(parent, v[i].node[0], v[i].node[1]) == 0) { //간선의 양 끝 정점이 같은 그룹에 속하면 사이클이라 걸러줌
UnionParent(parent, v[i].node[0], v[i].node[1]);
answer += v[i].distance;
}
}
return answer;
}