| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 스택
- 완전 탐색
- 클래스
- SSAFY
- 분할 정복
- MST
- dfs
- 링크드리스트
- 순열
- 큐
- 그리디
- DP
- 문자열
- BeautifulSoup
- 시뮬레이션
- 백트래킹
- BFS
- 중복 순열
- 우선순위 큐
- Knapsack
- 재귀
- 크루스칼
- 조합
- 메모리풀
- lis
- 빠른 입출력
- 이분 탐색
- 세그먼트 트리
- 비트마스크
- 피보나치 수
- Today
- Total
작심 24/7
[백준] 17779번 게리맨더링 2 본문
17779번: 게리맨더링 2
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름��
www.acmicpc.net
경계의 길이 d1과 d2의 길이가 각각 1부터 N-1까지일 때 만들 수 있는
꼭짓점 A, B, C, D를 기준으로 나누어진
1, 2, 3, 4, 5 선거구의 인구수를 구해야 한다.
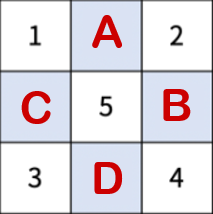
한 칸을 꼭짓점 A라 할 때,
이 점을 기준으로 나머지 꼭짓점 B, C, D도 만들어
최소 한 번이라도 다섯 선거구로 나눌 수 있는 조건을 만족시키는 칸은
파란색 경계선 안의 칸들이다.
빨간색으로 표시된 칸들은 B, C, D 세 점 모두를 만들 수 없는 경우
즉,
다이아몬드 모양의 경계선이 완성될 수 없는 경우이므로
파란색 범위 안의 칸들만 탐색해야 한다.

각 칸의 좌표는 A의 좌표이고
d1이 1일 때, d2가 1부터 N-1일 때,
d1이 2일 때, d2가 1부터 N-1일 때,
...
d1이 N-1일 때, d2가 1부터 N-1일 때
될 수 있는 B, C, D의 좌표를 구한다.
B, C, D의 좌표가 재현시의 범위를 벗어나면 선거구를 나눌 수 없는 경우이므로
그다음 길이로 넘어가고
벗어나지 않는다면 5개의 선거구로 나눌 수 있는 경우이므로
각 선거구의 인구수를 계산해준다.

이 표를 예로 들자면
파란색 화살표는 직사각형 형태이므로 그냥 for문으로 값을 구할 수 있고
초록색 화살표는 계단식 형태이므로 값의 범위를 늘리거나 줄이며 for문을 돌려야 한다.
이렇게 1, 2, 3, 4 선거구의 인구수를 구한 뒤
전체 인구수에서 이 값들을 빼면 5 선거구의 인구수가 된다.
여기서 인구가 가장 많은 선거구와 가장 적은 선거구의 인구수 차를 구하고
그 값의 최솟값을 갱신해준다.
#include <iostream>
#include <algorithm>
using namespace std;
int N, total, arr[21][21];
int Ax, Ay, Bx, By, Cx, Cy, Dx, Dy, A, B, C, D, E, Max = 0, Min = 50000, res = 50000;
int main() {
cin >> N;
for (int i = 0; i < N; i++) for (int j = 0; j < N; j++) cin >> arr[i][j], total += arr[i][j];
for (int i = 0; i < N - 2; i++) {
for (int j = 1; j < N - 1; j++) {
for (int d1 = 1; d1 < N; d1++) {
Ax = i, Ay = j, Cx = Ax + d1, Cy = Ay - d1;
if (Cx < 0 || Cy >= N) break;
for (int d2 = 1; d2 < N; d2++) {
Bx = Ax + d2, By = Ay + d2, Dx = Cx + d2, Dy = Cy + d2;
if (Bx < 0 || By >= N || Dx < 0 || Dy >= N) break;
int cnt = 0;
for (int m = 0; m < Ax; m++) for (int n = 0; n < Ay + 1; n++) A += arr[m][n];
for (int m = Ax; m < Cx; m++) {
for (int n = 0; n < Ay - cnt; n++) A += arr[m][n];
cnt++;
}
cnt = 0;
for (int m = 0; m < Ax + 1; m++) for (int n = Ay + 1; n < N; n++) B += arr[m][n];
for (int m = Ax + 1; m < Bx + 1; m++) {
for (int n = Ay + 2 + cnt; n < N; n++) B += arr[m][n];
cnt++;
}
cnt = 0;
for (int m = Dx; m < N; m++) for (int n = 0; n < Dy; n++) C += arr[m][n];
for (int m = Cx; m < Dx; m++) {
for (int n = 0; n < Cy + cnt; n++) C += arr[m][n];
cnt++;
}
cnt = 0;
for (int m = Dx + 1; m < N; m++) for (int n = Dy; n < N; n++) D += arr[m][n];
for (int m = Bx + 1; m < Dx + 1; m++) {
for (int n = By - cnt; n < N; n++) D += arr[m][n];
cnt++;
}
E = total - A - B - C - D;
Max = max(A, max(B, max(C, max(D, E))));
Min = min(A, min(B, min(C, min(D, E))));
res = min(res, Max - Min);
A = B = C = D = E = 0;
}
}
}
}
cout << res;
return 0;
}'백준' 카테고리의 다른 글
| [백준] 19237번 어른 상어 (0) | 2020.08.03 |
|---|---|
| [백준] 17837번 새로운 게임 2 (0) | 2020.07.31 |
| [백준] 9202번 Boggle (0) | 2020.07.27 |
| [백준] 2042번 구간 합 구하기 (0) | 2020.07.23 |
| [백준] 17143번 낚시왕 (0) | 2020.07.20 |